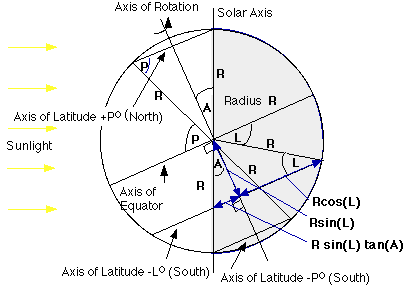
figure 1
Suppose we live on a Latitude of L degrees (The Gold Coast is at a latitude of about 28 degrees South of the equator... it is also on Earth). A "Latitude" on the surface of a planet is a circle on its surface where a radius from every point on it to the centre makes an angle of L degrees with the equatorial plane of the planet... sort of a parallel circle to the equator:

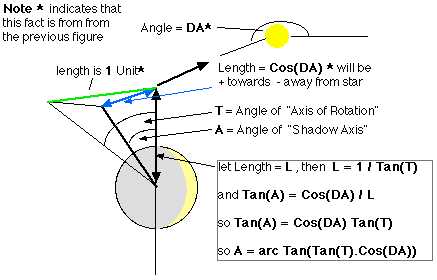
Figure 1 shows a cross section of a planet of radius R (6,400 km for Earth) with some algebra relevant to latitude L ...well one of the latitude L's, our L is the "downunder" one called South and rather unfairly "minus" on Earth. The "Solar Axis" is the axis perpendicular to the sun's (the planets star's) light, the planet actually rotates about an axis which is T degrees different from this and that axis is conveniently directly behind the "Solar Axis" in figure 1. Therefore in this diagram T is the same as A but as mentioned before this is only the case on a special occasion.
Another fact to note in figure 1 is that for latitudes bigger than a certain value, called P for "Polar" in figure 1, the latitude is either entirely in the dark (the Southern Hemisphere in figure 1) or entirely in the light (the Northern Hemisphere in figure 1) so we need to remember that +P and -P degrees are boundaries inside which the following Maths works and outside which it doesn't, much the same as the limitation that the latitudes can only lie between outside +90 and -90 degrees and still be on the planet!
There is a neat relationship between A degrees and P degrees and it is pretty easy to work out. Note that the triangle formed with base equal to the latitude P (either one, but the Northern one is drawn in in figure 1) and the centre of the circle, the arms of the triangle are both the same (equal to R the radius of the planet) and that the central angle of this (isoceles) triangle is 90-P+A degrees, the base angles are both P degrees (because of the isocelesnessosity!) of the triangle and all three add up to 180 degrees. Therefore
i.e. P + P + (90-P+A) = 180 so 90 + P + A = 180 so P + A = 90 so P = 90 - AThis means that P and A are complimentary angles. For Earth, the special case where the axial Tilt T = A (= 23.5 degrees) P will be the polar circles at 66.5 degrees, the limit of the 24 hour day in summer and 24 hour night in winter:
At this stage I am going to introduce some "preemptive retrospection", this is my term for discovering a problem in the derivation later on and then tracing it back to, in this case, around about here, and inserting the fix in such a way as to pretend that it is obvious to consider such things a priori... I have a hypothesis that the greater the haughtiness or "this is obvious..ness" of the justification the greater the actual mollification the author experienced when he she or it realised the blunder.
Ahemm... it is clearly obvious to any carbon based life form that the angle "A" can be negative as well as positive, as it will range from -T to +T degrees throughout the year, figures 3 and 4 (will) illustrate this. "A" will be positive when it leans the same way as the axial tilt and negative when it leans the other away. This means that the above representation of P is a special case where A is positive and P = 90-A, if A is negative then P would be 90+A to put these two exigencies together we use the modulus of A, written as |A| which is technically defined as +A for A >0 and -A for A < 0 so the general relationship between P and A is
|P| = 90 - |A|
The second clearly obvious thing is that the Latitude L is negative in the diagrams because it resides in the Southern Hemisphere. This is not important at this stage, but later, if L is considered positive, then the seasons are reversed! and indeed the formula generated needs to be measured, not from te Southern Winter Solstice, but the Summer one.
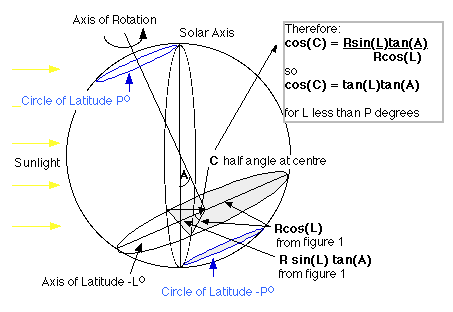
Figure 2 shows perspective of latitude L with the results form figure 1 incorporated in even more Algebra (remember this maths only applies for latitudes between +P and -P degrees). The purpose of both these pictures and the calculations is to figure out how much sunshine there is in proportion to darkness at latitude L
Following on from the calculation box in figure 2... to figure out the angle C we need to "un cosine" it, the is called "arc cos" or "inverse cos", it is a standard function on calculators and computers.
C = arc Cos(Tan(L)Tan(A))The angle defining the "Sector of sunshine" is actually 2 C. Now there are 360 degrees in a circle and if a day is H hours long (H=24 for Earth) then the number of sunshine hours is
2C.H C.H ---- = --- 360 180therefore
Sunshine Hours = (H/180) arc Cos(Tan(L)Tan(A)) (EQ 1)
but remember it is only when |L| < P
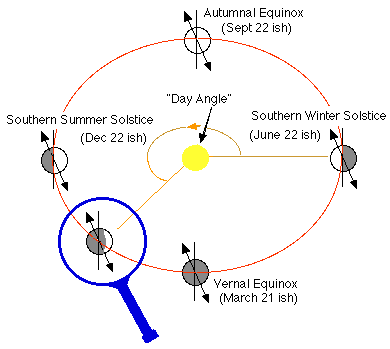
Figure 3 shows the planet at several times during the year (dates are for Earth!). Also note the parochial naming of the equinoxes by the Northerners ("up overs" ... I think they would like to call themselves). The IMPORTANT thing to note is how the axis of rotation (arrowed line) changes its orientation relative to the sunlight. I have defined the "Day Angle", DA for short, which relates to the number of days since the Southern Winter Solstice:
If the number of days per year is DY (365.25 for Earth) and the Day of the year D days since the Southern Winter Solstice then the "day angle" DA representing this day is given by
DA D --- = --- and so DA = D.360/DY (EQ 2) 360 DY
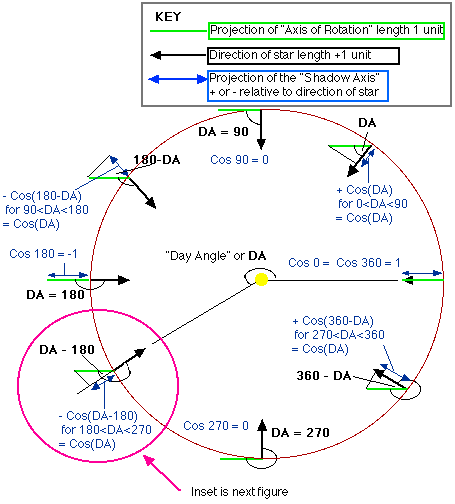
Figure 4 shows a detailed schematic view of figure 3 from above, the axial tilt angle is projected onto (a line through) the direction of the sun, this projection is directly related to the "Shadow Axis angle" A which is used above. Recall that A is the effective angle required in the "sunshine" calculation for any particular day. Figure 5, which is a perspective of a particular (but not special) day shows this relationship.
A = arc Tan(Tan(T).Cos(360.D/Y))Now recall the formula for Sunlight Hours (EQ 1), we can now substitute for A, the "Shadow axis angle"
Sunshine = (H/180) arc Cos(Tan(L)Tan(A)) (EQ 3)This is an important point in the derivation, because it is where we leave the angle A. Recall that the limit of applicability of the formula I am generating is +/- P = +/- (90 - |A|). However I will return to it to make the final formula into several slightly less terrifying parts. For the meantime...
we get a really horrible looking formula when we substitute for A
Sunshine = (H/180) arc Cos(Tan(L)Tan(arc Tan(Cos(360 D/Y)Tan(T)))Note however that we are tan-ing then immediately un tan-ing something to no net effect, so the formula can be "de taned" to become
Sunshine = (H/180) arc Cos(Tan(L)Cos(360 D/Y)Tan(T))You may find it neater, given that the limitations of the equations (|L| < 90-|A|) involve the shadow axis angle "A", to retain "A" in the final representation (that is EQ 3).
Given that A = arc Tan(Tan(T)Cos(360.D/Y)) Sunshine = (H/180) arc Cos(Tan(L)Tan(A)) when |A|-90 < L < 90-|A|
|L|=90-|A| which is the same as L = 90-|A| and L= |A| - 90
Sunshine = (H/180) arc Cos(Tan(90-|A|)Tan(A)) when 90-|A| < L < 90 and (H/180) arc Cos(Tan(|A|-90)Tan(A)) when -90 < L < -90+|A|At this point it useful to note that
Given that A = arc Tan(Tan(T)Cos(360.D/Y)) Sunshine... = (H/180) arc Cos(Tan(L)Tan(T)Cos(360.D/Y)) when A-90 < L < 90-A = 0 when L > 0 and H when L < 0 when 90-A < L < 90 = H when L > 0 and 0 when L > 0 when -90 < L < A-90
| Var | Meaning | Earth |
| H | Hours per day | 24 |
| L | Latitude | * |
| D | Days since the Southern Winter solstice | 22 June |
| DY | Days in a Year | 365.25 |
| T | Tilt of axis of rotation | 23.5 |
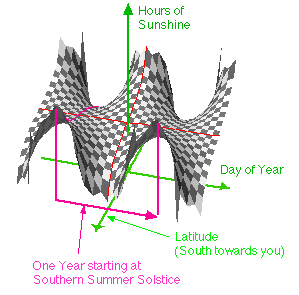
figure 6
shows a three dimensional view of the sunshine function.
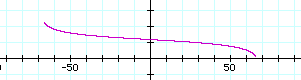
You've read the proof now see the movie: see the "Mexican wave" of sunshine hours varying horizontally with latitude and vertically with number of hours, the particular values used in this movie are brought to you by the planet Earth: The action covers the year depicted in figure 6 which has drawn on it, at the start of the year, the curve of figure 7. The scene opens on the Southern Summer Solstice. Note that on this day, the duration reaches 24 hours at -66.5 degrees, from there to the South pole any traveller will have 24 hour sunshine (on this day). Similar Northern polar bound persons will have 24 hours of dark. Only the curve within the bounds of |P| is drawn. Equatorial Earthlings experience the same 12 hours of sunshine each and every day. Click the picture to see and hear what happens next!
The movie is a quicktime movie, so if you are using a Windows computer (but for God's sake why?) then you will need to Download and add (as usual) yet another set of meaningless file names to your system for MPLAYER.EXE to show it thankfully this is small. Or install Quicktime. and the QTVR player for windows which is large.
Sunshine= (H/pi) arc Cos(Tan(L)Tan(T)Cos(2pi.D/DY))A good exercise is to make up a spreadsheet with this formula in it use references to other cells for the variables and don't forget to use the radians version because that is what spreadsheets use for angle measure.
Here is a formula for a spreadsheet, all angle measures in degrees.
| B1 | Hours per day |
| B2 | Latitude of place |
| B3 | Days since Southern Summer Solstice |
| B4 | Days per year |
| B5 | Axial Tilt |
By the way
The other big consideration is the fuzzy bit about the planet, the atmosphere refracts light to the extent that when you see the sun's lower rim touching the horizon, it is actually below the horizon.